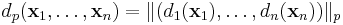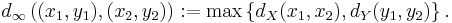Product metric

In mathematics, the product metric is a definition of metric on the Cartesian product of two metric spaces. As described below, the p product metric of the Cartesian product of n metric spaces is the p norm of the n-vector of the norms of the n subspaces:

$d_p(\mathbf{x}_1,\dots,\mathbf{x}_n) = \|(d_1(\mathbf{x}_1), \dots, d_n(\mathbf{x}_n))\|_p$

Definition

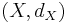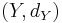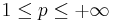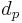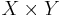Let $(X, d_{X})$ and $(Y, d_{Y})$ be metric spaces and let $1 \leq p \leq %2B \infty$ . Define the $p$ -product metric $d_{p}$ on $X \times Y$ by

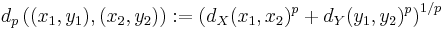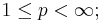
$d_{p} \left( (x_{1}, y_{1}) , (x_{2}, y_{2}) \right)�:= \left( d_{X} (x_{1}, x_{2})^{p} %2B d_{Y} (y_{1}, y_{2})^{p} \right)^{1/p}$ for $1 \leq p < \infty;$

$d_{\infty} \left( (x_{1}, y_{1}) , (x_{2}, y_{2}) \right)�:= \max \left\{ d_{X} (x_{1}, x_{2}), d_{Y} (y_{1}, y_{2}) \right\}.$

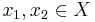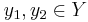for $x_{1}, x_{2} \in X$ , $y_{1}, y_{2} \in Y$ .

Choice of norm

For Euclidean spaces, using the L₂ norm gives rise to the Euclidean metric in the product space; however, any other choice of p will lead to a topologically equivalent metric space. In the category of metric spaces, the sup norm is used.

References

Deza, Michel Marie; Deza, Elena (2009), Encyclopedia of Distances, Springer-Verlag, p. 83, http://books.google.com/books?id=LXEezzccwcoC&pg=PA83 .